Capítulo 1

En los ejercicios 1 y 2, elimine los signos de agrupación y realice las operaciones.

1. $\hspace{0.1cm}a.\hspace{0.1cm}(5+4)\div{3}+(8-4)\div{2}\hspace{1cm}b.\hspace{0.1cm}3(5x+1)\\[1pt]$
$\hspace{0.1cm}c.\hspace{0.1cm}15(3x-2)+7(2x-1)-[7(2x+3)-4(x-1)]\begin{aligned} \\[10pt]\end{aligned}$
2. $\hspace{0.1cm}a.\hspace{0.1cm}500-[(5\cdot8)\div(4\cdot3)+16\cdot(10-2)]-5\\[10pt]$ $\hspace{0.1cm}b.\hspace{0.1cm}500-[(400\div8)\div(10\cdot5)-16\cdot(10\cdot2)]-181$

En los ejercicios 3 al 5, reduzca a la más mínima expresión.

3. $\hspace{0.1cm}a.\hspace{0.1cm}\cfrac{54}{108}\hspace{1cm}b.\hspace{0.1cm}\cfrac{12903}{16269}\begin{aligned} \\[20pt]\end{aligned}$
4. $\hspace{0.1cm}a.\hspace{0.1cm}\dfrac{12\cdot10\cdot35}{16\cdot14\cdot21}$

   $\hspace{0.1cm}b.\hspace{0.1cm}\dfrac{350\cdot120\cdot400}{1000\cdot50\cdot200}$

5. $\hspace{0.1cm}a.\hspace{0.1cm}\cfrac{28}{36}\cdot\cfrac{54}{108}\hspace{0.5cm}b.\hspace{0.1cm}\cfrac{28}{36}\div\cfrac{54}{108}\begin{aligned} \\[20pt]\end{aligned}$

En los ejercicios 6 al 10, encuentra el m.c.m y el MCD de los números indicados.

6. $\hspace{0.1cm}\hspace{0.1cm}208, 910 \wedge 1690\begin{aligned} \\[5pt]\end{aligned}$
7. $\hspace{0.1cm}\hspace{0.1cm}360, 480, 500 \wedge 600\begin{aligned} \\[5pt]\end{aligned}$
8. $\hspace{0.1cm}\hspace{0.1cm}30, 60 \wedge 90\begin{aligned} \\[5pt]\end{aligned}$
9. $\hspace{0.1cm}\hspace{0.1cm}136, 180 \wedge 240\begin{aligned} \\[5pt]\end{aligned}$
10. $\hspace{0.1cm}\hspace{0.1cm}45, 150 \wedge 180\begin{aligned} \\[5pt]\end{aligned}$

En los ejercicios 11 al 15, efectúe las operaciones indicadas y simplifique.

11. $\hspace{0.1cm}a.\hspace{0.1cm}\cfrac{3}{4}-\cfrac{5}{8}+\cfrac{7}{12}\begin{aligned} \\[5pt]\end{aligned}$

$\hspace{0.1cm}b.\hspace{0.1cm}14-2\dfrac {3}{16}-\dfrac {1}{8}+\dfrac{5}{6}$

12. $\hspace{0.1cm}a.\hspace{0.1cm}2\cfrac{3}{4}-3\cfrac{5}{8}+4\cfrac{7}{12}\begin{aligned} \\[5pt]\end{aligned}$

$\hspace{0.1cm}b.\hspace{0.1cm}9-\dfrac {3}{16}+3\dfrac {1}{8}+2\dfrac{5}{6}$

13. $\hspace{0.1cm}a.\hspace{0.1cm}\cfrac{3}{4}\div\left(\cfrac{5}{8}+2\cfrac{7}{12}\right)\begin{aligned} \\[5pt]\end{aligned}$

$\hspace{0.1cm}b.\hspace{0.1cm}9-\dfrac {3}{16}\cdot\left(3\dfrac {1}{8}+2\dfrac{5}{6}\right)$

14. $\hspace{0.1cm}a.\hspace{0.1cm}\cfrac{7}{3}\cdot3\cfrac{5}{8}\div\cfrac{7}{5}\begin{aligned} \\[5pt]\end{aligned}$

$\hspace{0.1cm}b.\hspace{0.1cm}9\left(\dfrac {3}{16}\div3\dfrac {1}{8}\right)+2\dfrac{5}{6}$

15. $\hspace{0.1cm}\hspace{0.1cm}\cfrac{10}{3}-4\left(\cfrac{8}{3}-\cfrac{6}{5}\right)\begin{aligned} \\[5pt]\end{aligned}$

En los ejercicios 16 al 19, dados los intervalos:

16. $\hspace{0.1cm}a.\hspace{0.1cm}A\cup B$

$\hspace{0.1cm}b.\hspace{0.1cm}B\cup C$

17. $\hspace{0.1cm}a.\hspace{0.1cm}A\cup B\cup C$

$\hspace{0.1cm}b.\hspace{0.1cm}A\cap B\cap C$

18. $\hspace{0.1cm}a.\hspace{0.1cm}A\cap B$

$\hspace{0.1cm}b.\hspace{0.1cm}B\cap C$

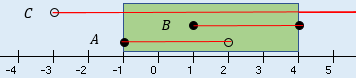
19. La siguiente gráfica, representa:
$$$$

$\hspace{0.1cm}a.\hspace{0.1cm}A\cup B\cup C$

$\hspace{0.1cm}b.\hspace{0.1cm} B\cup C$

$\hspace{0.1cm}c.\hspace{0.1cm}A\cap B\cap C$

$\hspace{0.1cm}d.\hspace{0.1cm}A\cap B$

En los ejercicios 20 al 27, resuelva las operaciones y simplifique.

20. $\hspace{0.1cm}a.\hspace{0.1cm}\dfrac {2}{3}\left( 6-\dfrac {3}{2}\right)-2\dfrac{5}{6}\begin{aligned} \\[5pt]\end{aligned}$

$\hspace{0.1cm}b.\hspace{0.1cm}{\dfrac {2}{\dfrac {2}{3}}-\dfrac {\dfrac {2}{3}}{2}}-3\cfrac{5}{8}$

21. $\dfrac {\dfrac {2+\dfrac {2}{5}}{3}+\dfrac {5\dfrac {1}{4}}{\dfrac {3}{2}}}{\dfrac {3\dfrac {3}{5}}{\dfrac {1}{2}}-\dfrac {\dfrac {1}{4}}{\dfrac {1}{2}}}\cdot \left( 235\dfrac {1}{5}\div 4\dfrac {1}{5}\right)$

$\hspace{0.1cm}b.\dfrac {\dfrac {1}{5}+2\dfrac {1}{3}}{\dfrac {3\dfrac {1}{7}}{\dfrac {2}{3}}-\dfrac {\dfrac {7}{2}}{\dfrac {3}{8}}}+\dfrac {\dfrac {1}{2}-\dfrac {1}{4}}{2\dfrac {1}{4}}$

22. $\hspace{0.1cm}a.\hspace{0.1cm}\dfrac {\dfrac {2}{5}+\dfrac {1}{2}}{\dfrac {1}{10}+\dfrac {3}{15}}\begin{aligned} \\[5pt]\end{aligned}$

$\hspace{0.1cm}b.\hspace{0.1cm}0.25\left( \dfrac {8}{9}-\dfrac {1}{2}\right)$

23. $\hspace{0.1cm}a.\dfrac {\dfrac {1}{5}\cdot 2\dfrac {1}{3}}{\dfrac {3\dfrac {1}{7}}{\dfrac {2}{3}}\div\dfrac {\dfrac {7}{2}}{\dfrac {3}{8}}}\cdot\dfrac {\dfrac {1}{2}\div\dfrac {1}{4}}{2\dfrac {1}{4}}$

$\hspace{0.1cm}b.\dfrac {\dfrac {1}{5}-2\dfrac {1}{3}}{\dfrac {3\dfrac {1}{7}}{\dfrac {2}{3}}+\dfrac {\dfrac {7}{2}}{\dfrac {3}{8}}}-\dfrac {\dfrac {1}{2}+\dfrac {1}{4}}{2\dfrac {1}{4}}$

24. $\hspace{0.1cm}a.\hspace{0.1cm}1-\left[ \dfrac {3}{2}\cdot 5-\dfrac {1}{2}\left( \dfrac {2}{3}+\dfrac {1}{9}\right) \right]\\[10pt]$ $\hspace{0.1cm}b.\hspace{0.1cm}\dfrac {1}{3}\left[ \dfrac {2}{4}-\left( \dfrac {5}{6}+\dfrac {1}{3}+\dfrac {3}{4}\right) +\dfrac {2}{5}\div \dfrac {3}{10}\right]$

25. $\hspace{0.1cm}a.\hspace{0.1cm}1+\dfrac {8}{3}\left( \dfrac {3}{4}\right) +\left\{ 2+\left[ \dfrac {3}{4}+1-\dfrac {2}{5}\left( +10-\dfrac {15}{4}\right) +1\right] \right\}\\[10pt]$ $\hspace{0.1cm}b.\hspace{0.1cm}\left[ \left( 2+\dfrac {3}{2}+4\right) \left( 5-\dfrac {1}{3}-4\right) \right] \div \left[ \left( \dfrac {5}{4}+3\right) \left( \dfrac {2}{3}-1\right) \right]$
26. $\hspace{0.1cm}a.\hspace{0.1cm}\dfrac {11}{121}\div \left\{ \dfrac {150}{3}-\dfrac {1}{2}-\dfrac {12}{6}\div \dfrac {\left( -8\right) }{2}-\dfrac {1000}{6}\cdot \dfrac {6}{50}\right\} -\dfrac {1000}{50}\\[10pt]$ $\hspace{0.1cm}b.\hspace{0.1cm}\dfrac {15}{225}\div \left( \dfrac {121}{11}-\dfrac {1}{3}-\dfrac {13}{26}\cdot \dfrac {\left( -8\right) }{16}-\dfrac {1}{63}\cdot \dfrac {63}{3}\right) \left( \dfrac {1}{-1-\dfrac {1}{2}}\right)$
27. $\hspace{0.1cm}a.\hspace{0.1cm}1-\dfrac {8}{3}\left( -\dfrac {3}{4}\right) -\left\{ 2-\left[ \dfrac {3}{4}-1+\dfrac {2}{5}\left( -10+\dfrac {15}{4}\right) -1\right] \right\}\\[10pt]$ $\hspace{0.1cm}b.\hspace{0.1cm}\left[ \left( 2-\dfrac {3}{2}-4\right) \left( 5+\dfrac {1}{3}+4\right) \right] \div \left[ \left( \dfrac {5}{4}-3\right) \left( \dfrac {2}{3}+1\right) \right]$

En los ejercicios del 28 al 35, plantea y resuelve los problemas de aplicación.

28. $\hspace{0.1cm}$Si estudiaste $2\dfrac{3}{4}$ de horas y tus hermanos estudiaron $4\dfrac{1}{5}$ y $7$ horas respectivamente,¿Cuántas horas han estudiado los tres juntos?.
29. $\hspace{0.1cm}$Un hombre vende $\dfrac{1}{3}$ de su finca, alquila $\dfrac{1}{8}$ y el resto lo cultiva. ¿Qué porción de la finca cultiva?.
30. $\hspace{0.1cm}$Si recorres 900 m, que son los 3/4 del camino de tu casa a la universidad. ¿Qué distancia hay de tu casa a la universidad?.

31. $\hspace{0.1cm}$El ácido sulfúrico contiene en peso $2$ partes de hidrógeno, $32$ partes de azufre y $64$ partes de oxígeno. ¿Qué fracción de ácido sulfúrico es el azufre?.
32. $\hspace{0.1cm}$Acabas de hacer un viaje familiar en tu carro particular, por lo que llenastes el tanque full de combustible. Si el trayecto del recorrido lo reaalizaste en dos tramos y se sabe que en el primero se consumieron $\dfrac{2}{3}$ de la gasolina que tenías y en el segundo la mitad de lo que le quedaba. ¿Cuántos galones tenía el tanque al iniciar el viaje? y ¿Cuántos galones se consumieron en cada tramo?, si al final del recorrido aún te quedaban 5 galones.

En los ejercicios 33 y 35, resolver los problemas utilizando regla de tres.

33. $\hspace{0.1cm}$Una cuadrilla de obreros ha hecho una obra en 20 días trabajando 6 horas diarias. ¿En cuántos días harían la misma obra trabajando 8 horas diarias?.
34. $\hspace{0.1cm}$Una guarnición de 1600 hombres tiene víveres para 10 días a razón de 3 raciones diarias cada hombre. Si se refuerzan con 400 hombres, ¿cuántos días duraran los víveres si cada hombre toma dos raciones diarias?.
35. Once $(11)$obreros labran un campo rectangular de 220 m de largo y 48 de ancho en 6 días. ¿Cuántos obreros serán necesarios para labrar otro campo análogo de 300 m de largo por 56 m de ancho en cinco días?.